Chiều cao hình thoi: Tìm hiểu công thức và cách tính nhanh nhất

Trong môn Toán, chúng ta có thể gặp nhiều hình tứ giác khác nhau và hình thoi là một trong những hình khá thú vị. Hình thoi có bốn cạnh bằng nhau, hai cặp cạnh song song và đường chéo cắt nhau tại góc vuông. Vậy đường cao trong hình thoi là gì, và tại sao nó lại quan trọng? Bài viết này sẽ giúp các bạn học sinh tìm hiểu khái niệm đường cao hình thoi, ý nghĩa, cách tính cũng như một số tính chất đặc biệt liên quan.

Khái Niệm Về Đường Cao Hình Thoi

Hình thoi là một tứ giác có bốn cạnh bằng nhau và hai cặp cạnh đối diện song song.

Đường cao (hay chiều cao) của hình thoi là đoạn thẳng được kẻ vuông góc từ một đỉnh (hoặc một cạnh) xuống cạnh đối diện.

Đường cao giúp ta biết được khoảng cách ngắn nhất giữa hai cạnh đối diện, đồng thời là yếu tố quan trọng để tính diện tích.

Đối với các bạn học sinh, việc tìm hiểu đường cao trong hình thoi là bước khởi đầu để hiểu sâu hơn về các khái niệm hình học sau này, đồng thời rèn luyện khả năng tư duy và giải quyết vấn đề.

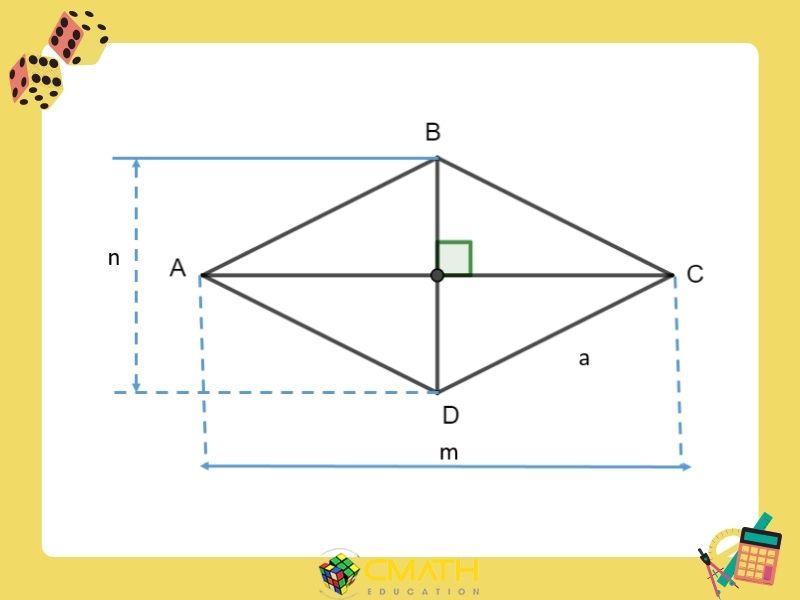
Cách Xác Định Đường Cao Trong Hình Thoi

Đường cao trong hình thoi rất quan trọng, dùng để tính diện tích và giải các bài toán liên quan. Dưới đây là ba bước cơ bản để xác định đường cao:

Bước 1: Xác định các đỉnh và cạnh của hình thoiHãy đánh dấu bốn đỉnh của hình thoi là A, B, C, D sao cho AB = BC = CD = DA. Đây là điều kiện để hình thoi có bốn cạnh bằng nhau.

Bước 2: Vẽ và xác định đường chéoTừ các đỉnh vừa xác định, vẽ hai đường chéo AC và BD. Hai đường chéo này sẽ cắt nhau tại một điểm (thường gọi là O) và vuông góc với nhau. Điểm O là trung tâm của hình thoi, chia mỗi đường chéo thành hai phần bằng nhau.

Bước 3: Xác định đường caoChọn một đỉnh (ví dụ đỉnh A), sau đó hạ một đoạn thẳng vuông góc xuống cạnh đối diện (cạnh CD). Đoạn thẳng này chính là đường cao của hình thoi. Đường cao không chỉ giúp tính diện tích mà còn giúp chúng ta giải nhiều bài toán liên quan đến đối xứng hoặc tính chất hình học khác.

Phương Pháp Tính Đường Cao Hình Thoi

Dùng công thức diện tích dựa trên cạnh và đường cao

• Diện tích (S) của hình thoi có thể tính bằng công thức: S = a × h
• Nếu biết trước diện tích S và độ dài cạnh a, ta tìm được đường cao h = S / a.

Ví dụ: Một hình thoi có diện tích 50 cm² và cạnh dài 10 cm. Khi đó, h = 50 / 10 = 5 cm. Vậy đường cao là 5 cm.

Dựa vào công thức diện tích theo hai đường chéo

• Hình thoi cũng có công thức diện tích: S = 1/2 × d₁ × d₂
• Khi biết hai đường chéo (d₁, d₂) và độ dài cạnh a, ta có thể tính được S, sau đó suy ra đường cao qua công thức h = S / a (nếu đề bài cho đủ dữ kiện).

Ví dụ: Hình thoi có d₁ = 8 cm, d₂ = 6 cm ⇒ S = 1/2 × 8 × 6 = 24 cm². Nếu cạnh a = 6 cm, thì h = 24 / 6 = 4 cm.

Sử dụng góc giữa hai cạnh

• Nếu biết cạnh a và góc α giữa hai cạnh kề, đường cao được tính bằng: h = a × sin(α).

Ví dụ: Hình thoi có cạnh 10 cm, góc α = 30°. Khi đó, h = 10 × sin(30°) = 10 × 1/2 = 5 cm.

Các Tính Chất Đặc Biệt của Đường Cao trong Hình Thoi

Đường cao hình thoi có nhiều tính chất thú vị khi xét đến hình dạng và góc của hình thoi:

• Khi góc nhọn, góc tù: Đường cao nằm bên trong hình, là đoạn vuông góc ngắn nhất giữa hai cạnh.
• Khi hai đường chéo bằng nhau (hình vuông): Đường cao bằng chính cạnh của hình thoi, vì hình thoi lúc này là hình vuông.
• Đường cao thay đổi theo góc: Nếu cạnh giữ nguyên mà góc thay đổi, độ dài đường cao cũng thay đổi.

Cmath - Trung Tâm Dạy Toán Uy Tín với Đội Ngũ Giáo Viên Giỏi

Tại Cmath, chúng mình luôn chú trọng chất lượng dạy học và mong muốn mang lại cho học sinh những giờ học toán vui vẻ, hiệu quả:

• Đội ngũ giáo viên dày dặn kinh nghiệm: Thầy cô tại Cmath đã có nhiều năm giảng dạy và nghiên cứu trong lĩnh vực giáo dục tiểu học. Các thầy cô hiểu rõ tâm lý, khả năng tiếp thu của học sinh lớp 4 và biết cách truyền đạt kiến thức một cách gần gũi, dễ hiểu.
• Phương pháp giảng dạy linh hoạt: Thay vì học thuộc lòng, Cmath khuyến khích học sinh khám phá bài học qua ví dụ minh họa, bài tập tương tác và trò chơi toán học. Điều này giúp các em xây dựng niềm yêu thích với toán và tiếp thu kiến thức sâu hơn.
• Chương trình học cập nhật: Nội dung bài giảng được thiết kế theo chuẩn kiến thức mới, bám sát chương trình và có mở rộng thêm phần tư duy logic. Các em vừa nắm vững lý thuyết vừa được rèn luyện kỹ năng giải quyết vấn đề.
• Môi trường học tập thân thiện: Cmath luôn tạo điều kiện để học sinh được trao đổi, đặt câu hỏi và thực hành thường xuyên, giúp các em hình thành sự tự tin và chủ động trong học tập.

>>> Xem ngay: Danh sách các khóa học của Cmath

Nếu bạn muốn tìm một nơi để khám phá thế giới toán học thật sinh động, hãy đến với Cmath để trải nghiệm phương pháp học hiện đại và gắn bó lâu dài với môn toán!

Hy vọng rằng bài viết này đã giúp các bạn học sinh hiểu rõ hơn về đường cao hình thoi: từ cách xác định, công thức tính, đến những tính chất đặc biệt. Chúc các bạn học tập thật tốt và luôn tìm thấy niềm vui trong việc khám phá toán học!