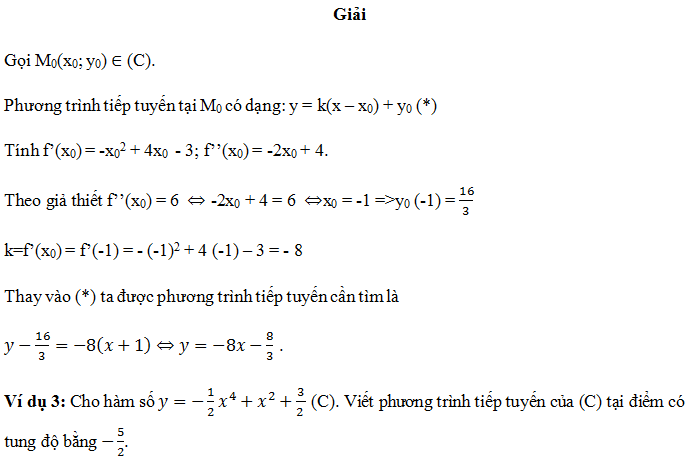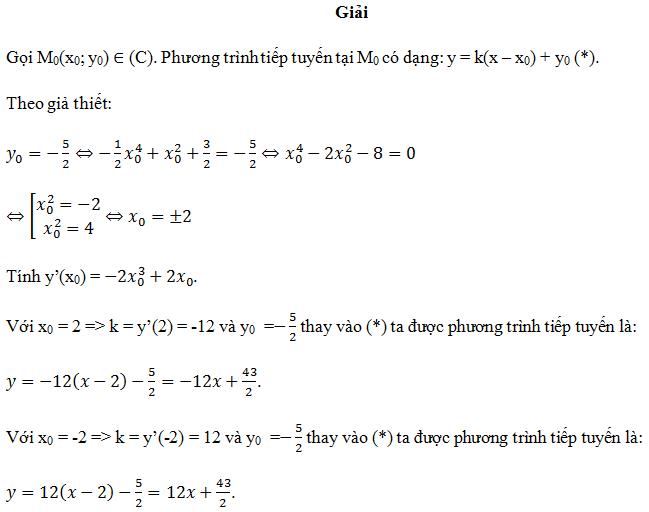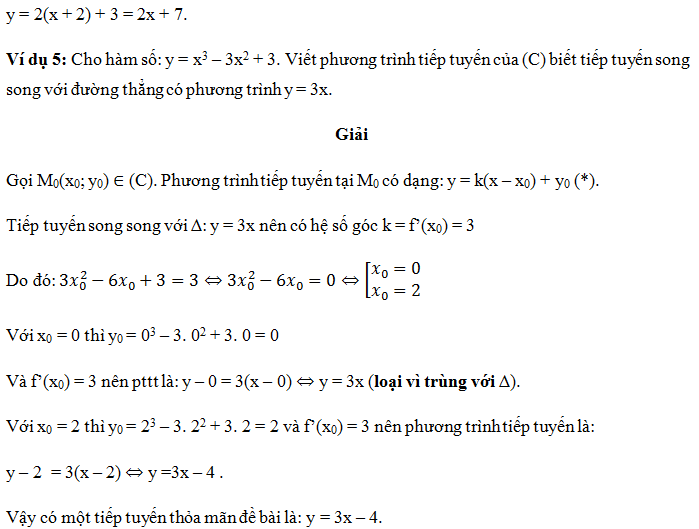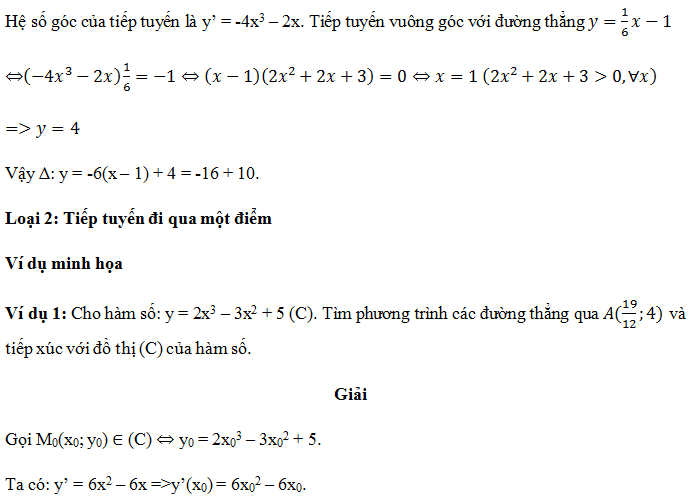I.Lý thuyết: Bài toán về tiếp tuyến với đường cong:
Cách 1: Dùng tọa độ tiếp điểm
Phương trình tiếp tuyến có dạng: y = f’(x0). (x - x0) + y0
1.Lập phương trình tiếp tuyến với đường cong tại điểm M(x0, y0) thuộc đồ thị hàm số (tức là tiếp tuyến duy nhất nhận M(x0; y0) làm tiếp điểm).
Phương trình tiếp tuyến với hàm số (C): y = f(x) tại điểm M(x0; y0) ∈ (C)
(hoặc tại h x = x0 ) có dạng: y =f’(x0).(x - x0) + y0.
2.Lập phương trình tiếp tuyến d với đường cong đi qua điểm A (xA, yA) cho trước, kể cả điểm thuộc đồ thị hàm số (tức là mọi tiếp tuyến đi qua A(xA, yA)).
Cho hàm số (C): y = f(x). Giả sử tiếp điểm là M(x0, y0), khi đó phương trình tiếp tuyến có dạng: y = f’(x).(x - x0) + y0 (d).
Điểm A(xA, yA) ∈ d, ta được: yA = f’(x0). (xA - x0) + y0 => x0
Từ đó lập được phương trình tiếp tuyến d.
3. Lập phương tiếp tuyến d với đường cong biết hệ số góc k
Cho hàm số (C): y = f(x). Giả sử tiếp điểm là M(x0;y0), khi đó phương trình tiếp tuyến có dạng: d: y = f’(x0).(x - x0) + y0.
Hoành độ tiếp điểm của tiếp tuyến d là nghiệm của phương trình:
f’(x0) = k => x0, thay vào hàm số ta được y0 = f(x0).
Ta lập được phương trình tiếp tuyến d: y = f’(x0). (x - x0) + y0.
Cách 2: Dùng điều kiện tiếp xúc
Phương trình đường thẳng đi qua một điểm M(x0; y0) có hệ số góc k có dạng;
d:y = g’(x) = k.(x - x0) + y0.
Điều kiện để đường thằng y = g(x) tiếp xúc với đồ thị hàm số y = f(x) là hệ phương trình sau có nghiệm: (left{begin{matrix} f(x)=g(x) & f'(x)=g'(x) & end{matrix}right.) Từ đó lập được phương trình tiếp tuyến d.
II. Bài tập
Loại 1: Cho hàm số y =f(x). Viết phương trình tiếp tuyến tại điểm M0(x0; y0) ∈ (C).
Giải
Phương trình tiếp tuyến tại M0 có dạng: y = k(x - x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k.
MỘT SỐ DẠNG CƠ BẢN
Dạng 1: Viết phương trình tiếp tuyến tại M0(x0;y0) ∈ (C)
-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc
Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.
Dạng 2: Cho trước hoành độ tiếp điểm x0
-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.
- Thay x0 vào hàm số ta tìm được tung độ tiếp điểm.
Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.
Dạng 3: Cho trước tung độ tiếp điểm y0
-Giải phương trình y0 = f(x0) để tìm x0.
-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.
Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.
Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.
Dạng 4: Cho trước hệ số góc của tiếp tuyến k = y’(x0) = f’(x0)
-Tính đạo hàm và giải phương trình k = y’(x0) = f’(x0) để tìm x0
- Thay x0 vào hàm số ta tìm được tung độ tiếp điểm cần tìm.
Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.
Chú ý: Một số dạng khác
-Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến vuông góc với đường thẳng : y = ax + b thì điều này
<=> y’(x0). a = -1 ⇔ y’(x0) = -1/a
... Quay về dạng 4.
- Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến song song với đường thẳng
y = ax + b thì điều này ⇔ y’(x0) = a… Quay về dạng 4.
- Khi giả thiết yêu cầu viết phương trình tiếp tuyến tại giao điểm với đường thẳng y = ax + b thì việc đầu tiên là tìm tọa độ giao điểm của (C) và đường thẳng… Quay về dạng 1.
Chú ý:
Cho hai đường thẳng d1: y = a1x + b1 với a1 là hệ số góc của đường thẳng d1 và y = a2x + b2 với a2 là hệ số góc của đường thẳng d2.