Previous post: Transformations of Functions: Translations
In the post linked above I described the change in how I’ve taught translations of functions with my year 11s and 12s by focusing on moving the coordinate plane rather than translating the function itself.
This post continues that idea by looking at reflections.
I find ‘reflections’ a bit of a misnomer when describing transformations, as we introduce them with lines of reflection, and modulus transformations focus on reflections, but this is the most common way students will come across these things in revision materials, textbooks etc.
I ‘see’ these transformations as rotations around an axis rather than a reflection, but in teaching I’ll focus on what’s changing (input or output?).
The gif below shows the animation in the slides at the bottom of the post.
The language is the key focus for students here. Even though I will use the word reflection (my own fussiness is hardly reason enough to alter it), I make sure I labour the point the x-axis values are not changing. Like with stretches later on, ‘in the x-axis’ being different to ‘in the x-direction’ will throw pupils not attending to the language closely. This is why I like to reinforce the changing y-values.
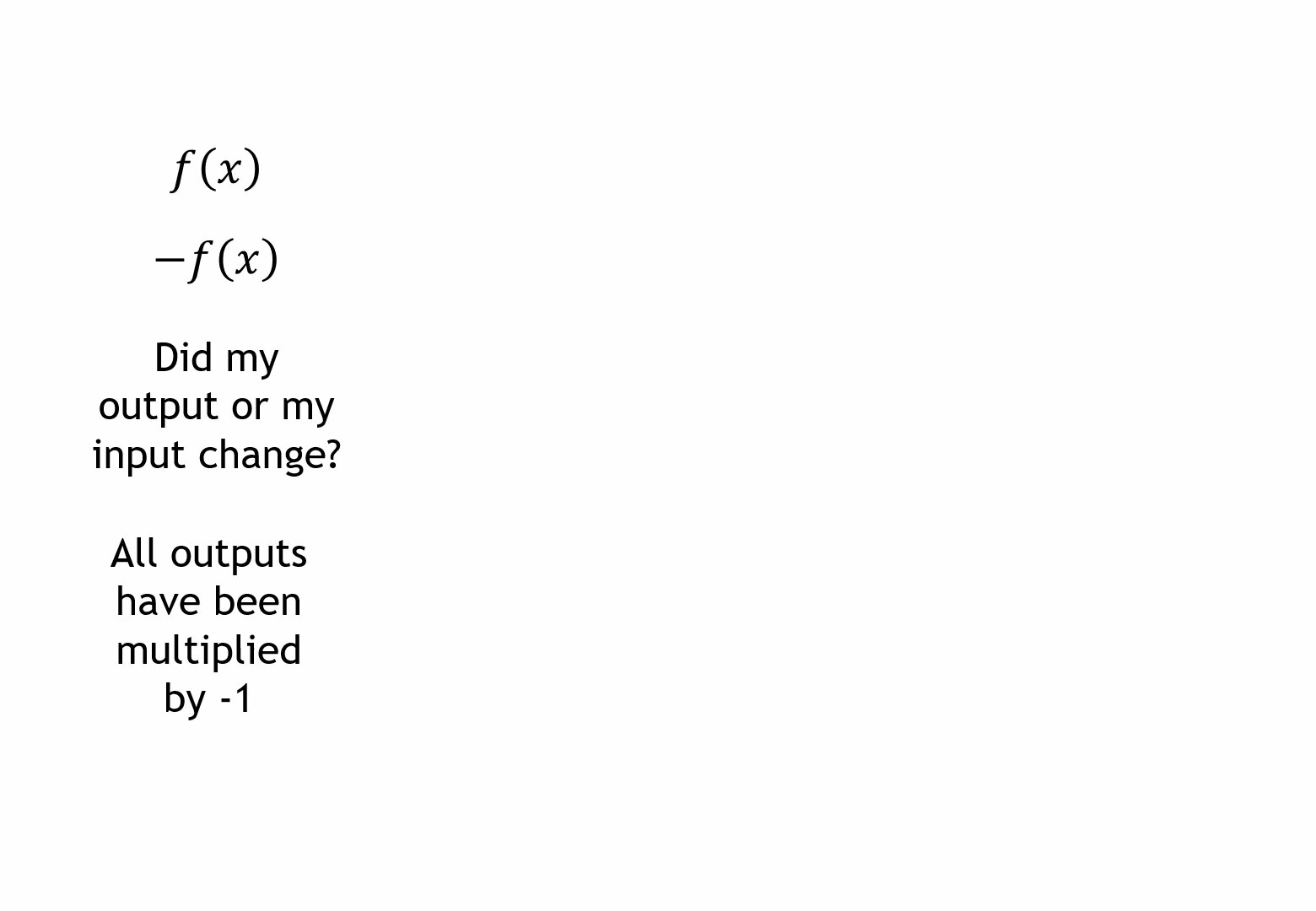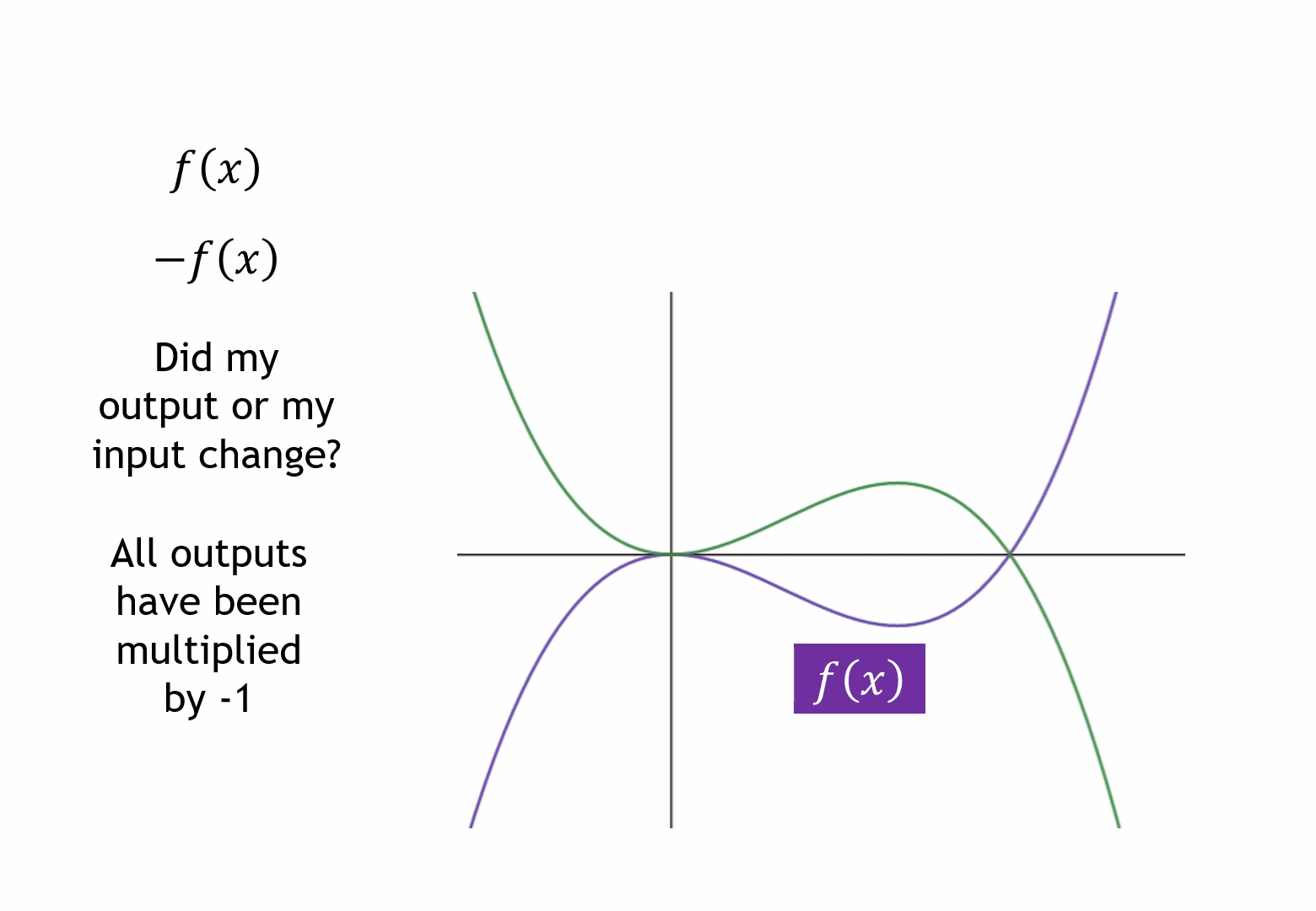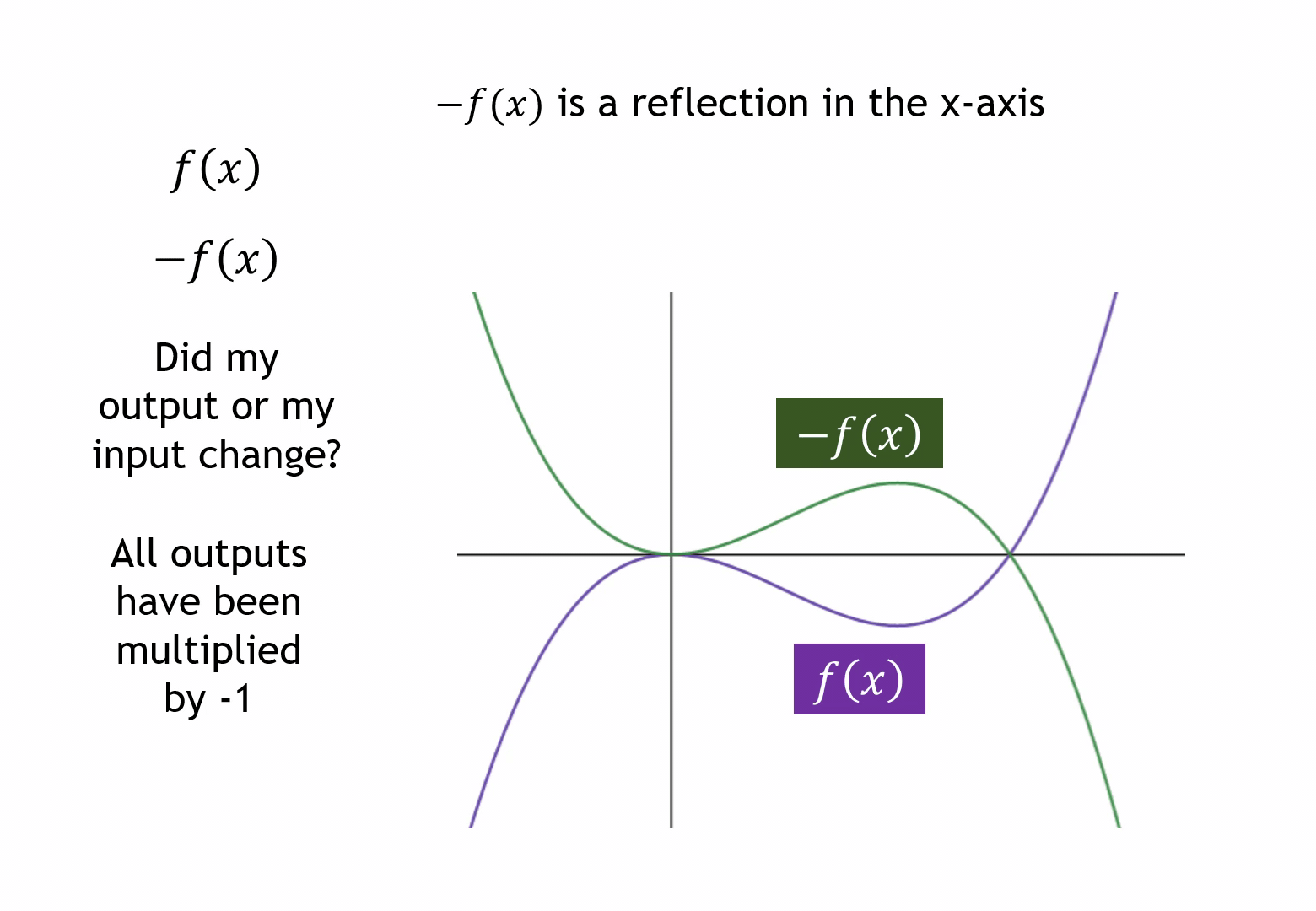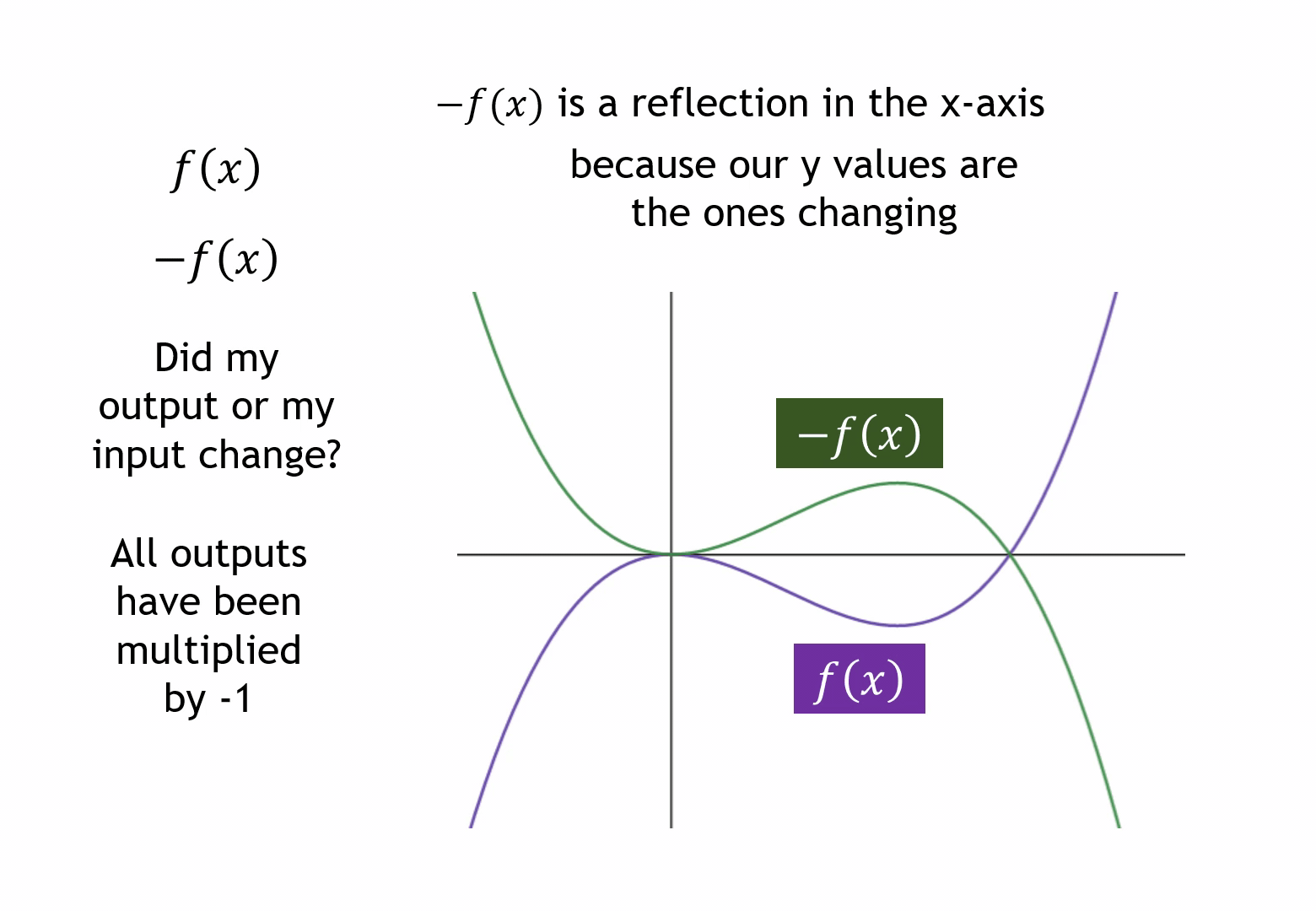
I’ve also started to introduce the idea of multiplying all y-values to sow the idea we’ll come to in stretches.
This process then repeats for changing the inputs.
And then again, as before, using this information to generalise.
Next I used two pieces of tracing paper, one with axes sketched and one with a function, and questioned pupils on the transformations that are happening.
Crude? Yes. But by layering them differently and asking pupils to reason what they think is happening when the axes move vs. where the function moves by flipping over one of the pieces of tracing paper, they can begin to visualise the different ways to ‘see’ a transformation beyond ‘it flips’. What’s the IT? What do you mean by a flip?
This could then consolidate translations as mentioned in the previous post because we’ve developed ways of thinking about movement of axes as well as movements of functions.
Before moving on to stretches, I wrote the following tasks to consolidate everything we’ve looked at so far.
I purposefully chose a function that’s a faff to express algebraically as I want them looking at the geometry of a transformation rather than the algebra of it. This was easy to set up in desmos using a cubic and sine wave with restricted domains.
The task is a mixture of translations, -f(x) and f(-x) and gives students the opportunity to consider what transformations get them back to position A from a given coordinate pair too.
The next task is more synoptic in that it brings together the straight line work we’d been doing at the start of the year and touching lightly on the trigonometry with their other teacher.
Students found this extremely challenging moving between different aspects of mathematics where the only thing in common is the coordinate grid and the function, and I’m pleased that we’re getting into the meat of bringing different topic areas together so it will be less of a shock come exam technique time.
There was lots of discussion and debate about the way the brackets impact question 4g, and it stretched the understanding of bracket use in function notation as well as a grouping for operations.
All animated slides shown above, and all tasks (with solutions) are here:


